| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- Multi threaded
- lidar
- Motion compensate
- Reflectivity
- Data Packet
- Alpha Prime
- 3-sigma rule
- Frame rate
- Data Race
- 센서셋
- Azimuth
- Phase Offset
- timestamp
- ApolloAuto
- Interference Pattern
- Single threaded
- PYTHON
- nvidia
- object detection
- Alpha Prime(VLS-128)
- VLS-128
- Phase Lock
- Coding Test
- coordinate system
- Quaternion 연산
- PointCloud Frame
- HDmap
- Smart Pointer
- PointCloud
- Veloview
- Today
- Total
엔지니어 동행하기
(코드 예제) XY평면에서 두 벡터의 사이각 계산 본문
두 벡터의 사이각(θ) 계산
v1, v2 벡터의 길이를 구하고 벡터 내적 정의를 이용해서 cosθ를 계산합니다. 마지막으로 arc cosine 함수를 이용해서 사이각을 구하면 됩니다. 벡터 길이를 구하는 구체적인 방법은 아래 블로그 글을 참고하면 됩니다.
https://kukuta.tistory.com/152
벡터(vector)의 크기(길이)
[이전] 포스트에서 벡터는 크기와 방향을 가진다고 했으며, 그중 크기(또는 길이)를 나타내는 것이 바로 벡터의 '길이'이다. v = 일 때, 벡터 v의 크기는 얼마인가? 대략 보면 답이 없다. 값 세 개로
kukuta.tistory.com
벡터 내적 정의는 아래와 같습니다.
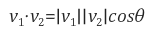
코드 예제
template <typename T>
T CalculateTheta2DXY(const Eigen::Matrix<T, 3, 1> &v1,
const Eigen::Matrix<T, 3, 1> &v2) {
T v1_len = static_cast<T>(sqrt((v1.head(2).cwiseProduct(v1.head(2))).sum()));
T v2_len = static_cast<T>(sqrt((v2.head(2).cwiseProduct(v2.head(2))).sum()));
if (v1_len < std::numeric_limits<T>::epsilon() ||
v2_len < std::numeric_limits<T>::epsilon()) {
return 0.0;
}
const T cos_theta =
(v1.head(2).cwiseProduct(v2.head(2))).sum() / (v1_len * v2_len);
const T sin_theta = (v1(0) * v2(1) - v1(1) * v2(0)) / (v1_len * v2_len);
T theta = std::acos(cos_theta);
if (sin_theta < 0.0) {
theta = -theta;
}
return theta;
}1. v1, v2 벡터의 길이를 계산
cwiseProduct : coefficient-wise product을 의미하며 대응하는 element 끼리 곱합니다.
2. v1의 길이가 0이거나 v2의 길이가 0인 경우 θ는 0.0 반환
2022.07.10 - [Modern C++] - std::numeric_limits::epsilon(), 0에 가까운 값, Floating Point비교
std::numeric_limits<T>::epsilon(), 0에 가까운 값, Floating Point비교
Floating Point 가 같은지 비교할 때, == operator를 사용하면 의도하지 않은 결과를 얻게 됩니다. 그 이유는 컴퓨터가 Floating Point를 정확히 그 값으로 가지고 있는 것이 아니라 그 값과 가장 가까운, 컴
engineer-sullivan.tistory.com
3. 벡터 내적 정의에 따라 cosθ 계산
4. 사이각 계산
θ = acos(cosθ) ( sinθ > 0일 때)
θ = -acos(cosθ) ( sinθ < 0일 때)
https://github.com/ApolloAuto/apollo/blob/master/modules/perception/common/geometry/basic.h
GitHub - ApolloAuto/apollo: An open autonomous driving platform
An open autonomous driving platform. Contribute to ApolloAuto/apollo development by creating an account on GitHub.
github.com
